Leonhard Euler
Bonjour à tous et bienvenue chez Graine de Génie ! Dans cet article, on déménage de la France du XVIIème siècle pour l’Angleterre du XVIIIème pour vous présenter Leonhard Euler, un important mathématicien qui a été très influencé par Pierre de Fermat lui-même ! Est-ce que vous vous en rappelez ? J’espère que oui…
Notre personnage principal d’aujourd’hui est né le 15 avril de 1707 en Suisse. Pourtant, il a passé la plupart de sa vie à Saint-Pétersbourg et à Berlin, où il a fait des contributions vraiment importantes aux branches de la théorie des nombres, du calcul et de la théorie des graphes.
Mais revenons au début de tout. Il a commencé ses études à l’université de Basilea à l’âge de 17 ans, où il a attiré l’attention de Johann Bernoulli, l’un des membres de la célèbre famille de mathématiciens de ce nom-là. Grâce à cela, il est parti vers Saint-Pétersbourg en 1727 afin de rejoindre le reste de la famille. Les mathématiciens Bernoulli sont devenus ainsi pas seulement des collègues mais aussi les amis les plus proches de Leonhard Euler.
C’est également en 1727 qu’il a découvert le nombre qui constitue la base des logarithmes népériens… cela vous dit quelque chose ? On parle du nombre e , qui a reçu cette appellation pour l’initial du nom de son découvreur. Il a défini la constante mathématique e comme le nombre réel tel que la valeur de la dérivée de la fonction f(x)= ex dans le point 0 est exactement égal à 1. C’est à dire f'(0)= e0 = 1 . Cela signifie que la pente de la droite tangente à la courbe de la fonction dans le point x=0 est 1. Au fait, c’est Euler qui a été le pionnier à utiliser la notation f(x) et f'(x) pour une fonction et sa dérivée, ce pour quoi tous les étudiant(e)s de mathématiques doivent le remercier puisqu’il a significativement facilité l’écriture du calcul. Mais ses contributions à cette branche des mathématiques ne finissent pas ici. En 1777, il a utilisé pour la première fois la notation i pour le nombre imaginaire √-1 . Ainsi, il commence une étude en profondeur des nombres complexes où il les met en relation avec les fonctions trigonométriques (fonction sinus et fonction cosinus), et qui conclut finalement avec la formule ei =cos + i sin pour un nombre réel quelconque. Est-ce que vous avez déjà vu cette formule ? Bon, sinon, je suis sûre que celle-ci vous semblera familière pour le cas particulier où = , puisque là on aura ei= cos + i sin et, en utilisant que sin = 0 et cos = -1 on arrive à ei= -1 + 0 , d’où ei+ 1 = 0 . Voilà ! Cette dernière est connue comme Identité d’ Euler, et c’est la formule que tous les nerds portent sur leurs Tee-Shirt (je m’inclus aussi). C’est joli non ? On a les deux nombres irrationnels les plus connus ( et e ), et le nombre complexe principal (i), tous dans la même formule ! C’est fascinant !
Cependant, Euler n’a été pionnier que dans l’analyse et les nombres complexes. En 1736, il a résolu le problème connu comme problème des points de Konigsberg, événement qui a donné lieu à la théorie des graphes. Mais on ne va pas vous faire attendre, et on va vous présenter tout de suite ce problème ! Leonhard Euler
L’ancienne ville de Koenigsberg (actuellement appelée Kaliningrad, en Russie) était traversée par la fleuve Pregel, qui formait une île au milieu appelée kneiphof, donnant lieu à quatre régions différenciées mais connectées par 7 points comme on peut le voir sur le dessin ci-dessous. Alors le problème demandait s’il était possible de parcourir à pied toute la ville en traversant seulement une fois chaque point et en arrivant finalement au point de début.
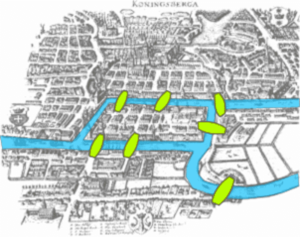
Qu’est-ce que vous en pensez ? La réponse est non et, pour le démontrer, Euler a fait un schéma de la situation en représentant les quatre régions comme des vertex dans le plan et les ponts comme des lignes qui les connectent. Ne vous inquiétez pas, j’ajoute ici un schéma afin que vous puissiez suivre l’explication. Ainsi, vous pourrez proposer ce défi à vos collègues, et vous vanter de votre intelligence en le résolvant après !
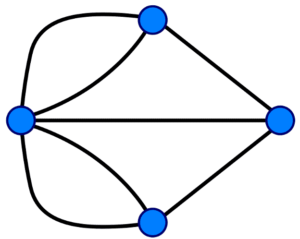
Alors, de cette manière, comme il faut passer seulement une fois par chaque ligne, chaque vertex doit être lié par deux ponts (l’un pour arriver et l’autre pour sortir). Et de même pour le point de départ puisque l’on nous dit que celui-ci doit être aussi le point d’arrivée. Ainsi, en ayant deux ponts connectés à chaque région, le nombre de ponts devrait être pair. En revanche, le nombre de ponts que l’on a est 7, et donc il est impossible de faire ce que le problème nous demande. Voilà ! C’est cool non ? J’espère que vous avez aimé cette énigme.
En fait, après ce problème et la résolution donnée par Euler, on a appelé cycle eulérien tout chemin présenté dans un schéma où l’on parcourt toutes les arêtes une seule fois et dont le point de départ coïncide avec le point d’arrivée.
Bon, je vous laisse vous reposer après ce défi, mais je vous attends la semaine prochaine avec une autre histoire aussi intéressante que celle-ci (ou peut-être plus encore). Venez nombreux et soyez prêts à résoudre les énigmes des mathématiques sur Graine de Génie. Bon courage et à bientôt !
